..

Swin transformers

  1. Features
  2. Architecture
  3. Working example
    1. Patch partition
    2. Linear embedding
    3. Swin transformer block
    4. Patch merging
  4. References

Features

  • Swin transformer can be used as a general purpose backbone for various computer vision tasks
  • It produces an embedding for the image
  • Earlier computer vision transformer architectures faced the problem of scalability as the computations are quadratic in nature
    • Quadratic in relation to number of tokens (N)
    • For images, this token size is high (based on # of patches)

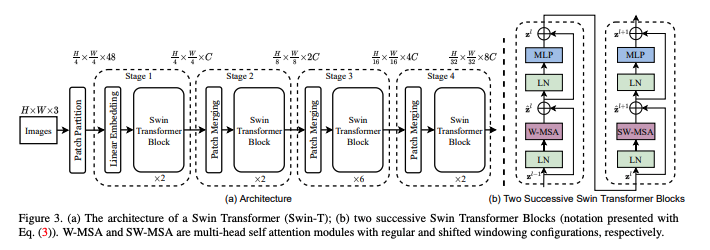
Architecture

The model has the following blocks

  1. Patch partition
  2. Linear embedding
  3. Swin transformer block
    1. Contains windowed multi-self attention (W-MSA) and shifted window multi-self attentions (SW-MSA)
  4. Patch merging image

Working example

Let’s consider a working example of one pass from each major block of the architecture. Consider input image of size: 32x32x3

Patch partition

  1. Divide the image into patches of 4x4x3 pixels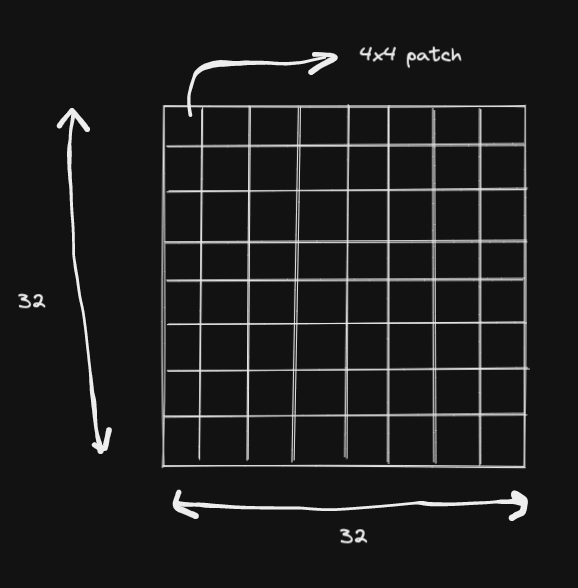
    1. image
    2. In total we will have: (32/4) * (32/4) = 64 patches.

Linear embedding

  1. Flatten each patch to a vector. In this case the vector dimension for each patch would be 4*4*3 = 48. This vector is converted to an arbitrary dimension (called as C in the paper) using a vanilla neural network. For our example, let’s consider C as 64
  2. After this, you would have an image of size (32/4) * (32/4) * 64
    1. The overall image dimensions (height and width) will be reduced and each patch will be replaced with a feature vector of dimension C.
    2. The image size is now: 8 x 8 x 64

Swin transformer block

  1. The image of above dimension is further divided into non-overlapping windows of M x M patches. M is the number of windows.
  2. For our example, let’s take M as 4
  3. Our window will contain 4 * 4 = 16 patches, each with dimension C as 64.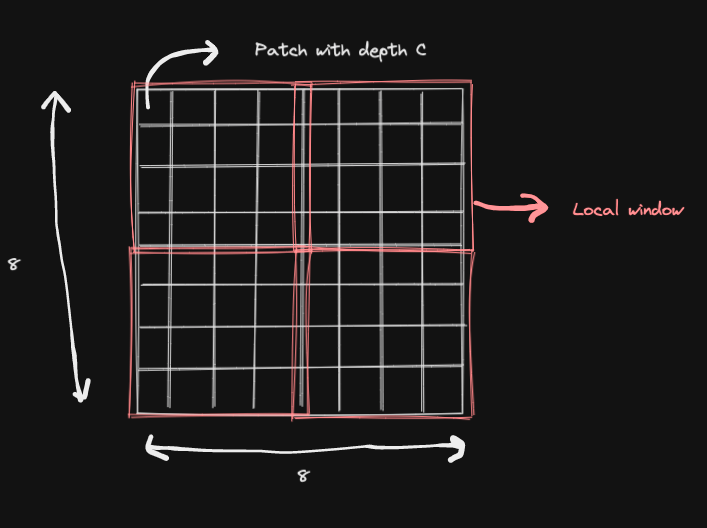
  4. image
  5. Self attention is computed locally within each window. For our case, that would mean, 16 * 16 = 256 dot products. Each patch attends to every other patch in the local window (i.e each patch attends to 16 other patches)
  6. Query and Key matrix will have the dimensions: 16 * d. d is the query/key dimension.
    1. Within a local window, Query matrix will only have 16 values
  7. This makes computation more scalable for large images and is called window based self attention
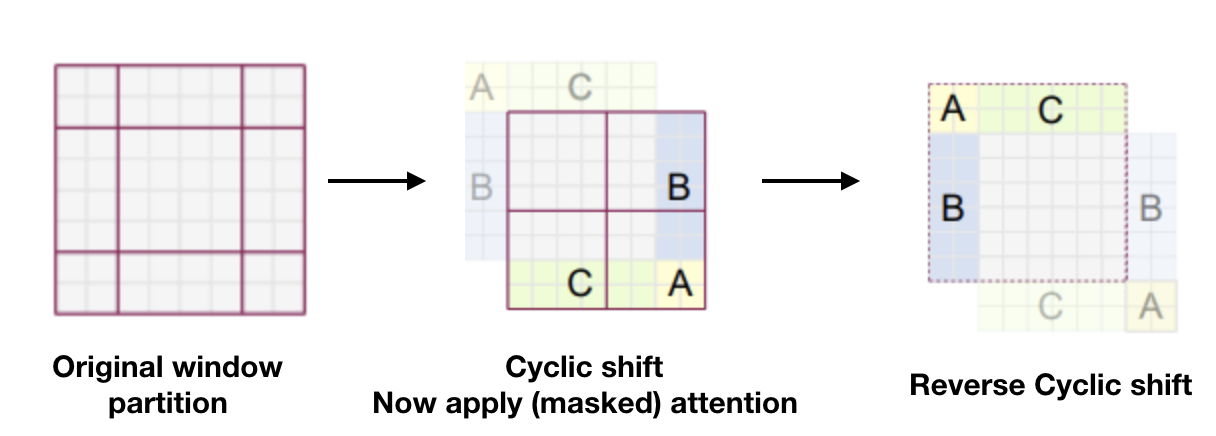
  8. Shift the windows to the bottom right by 2 patches. Compute self attention again.
    1. image

Patch merging

  1. Merge patches in 2x2 neighbourhood
  2. This means, that we concatenate features of all the patches in 2x2 neighbourhood. The resulting patch (or pixel) would now be of size 4C, i.e 256 in our example.
  3. A linear layer is applied to scale this back to 2C. i.e 128 for our example.
  4. After patch merging, our image would now be of size (8/2) * (8/2) * 2C i.e 4 x 4 x 128 for our example.

For a real life model: swin_large_patch4_window7_224_22kto1k

  • Patch size is 4
  • Window size (M) is 7
  • Input image size is 224 * 224 * 3

References

  1. Medium article
  2. Official paper